
本文力求通俗,从传输线开始到史密斯圆图,介绍了射频领域几个基础的概念,希望能给“欲渡无舟楫”的年轻射频从业者一块小小的浮木,也祝愿大家早日抵达属于自己的星辰大海。
当一个基带工程师和射频工程师同时来到Layout工程师这里,基带工程师对Layout工程师说,兄弟,我这根电源线再加宽点,要保证总电阻小于0.2欧姆。射频工程师对Layout工程师说,兄弟,我这根微带线也要加宽一点,第二层挖空,两侧0.2mm间距,保证阻抗为50欧。刚入行的基带工程师很困惑,心想用铜线盘出50欧阻值,那得多长呀?于是请教射频工程师,射频工程师说这叫特性阻抗,跟导体的电阻不一样,接连便是更难懂的话,什么“分布参数”,什么“根号下L/C”之类。年轻的基带工程师略带尴尬地点了点头,心想,他说的欧姆和我说的欧姆是一个东西吗?
是也不是!
笔者本人小时候家里看的是有线电视(暴露年龄),有线电视的那根“有线”看起来就像下图一样:
上初中的我一眼就注意到上面赫然印着“75ohm”字样,同时也注意到这根线的长度并不固定,那么如何能断言阻抗就是75欧呢?另外,如果家里有两台电视,需要使用一个叫“分线器”的一进两出的小盒子,而不能直接破线做Y形连接,于是年少的我发扬了不求甚解的优良传统,把这个问题归结为“未曾学到的知识”而置之不理。
直到参加工作后才开始直面这个问题,首先我们要明确的是,从量纲的角度,特性阻抗说的“欧姆”和电阻器的单位“欧姆”并无不同,都是表示电压(伏特)和电流(安培)的比值,电阻器的伏安特性被欧姆定律总结得非常清晰明了,我们在初中就学过。那么特性阻抗说的50欧或者75欧是什么电压和什么电流的比呢?
原来用特性阻抗描述的对象不是“导线”或者“导体”,而是“传输线”,传输线是用来传输电磁波的线状结构,传输线一般来说有几个很重要的特点,也是我们讨论特性阻抗的前提:
01至少由两根导体组成,比如说“平行线”就是两条导线,“同轴线”由圆筒状的外壳和细长的芯线组成,“微带线”由导体参考平面和一根扁长的导线组成。实际使用中,我们通常把其中一根导体接地,另一根作为承载信号的线。
02传输线是细长的线状结构,有特定的信号传输方向即正反两个信号传输方向,传输线一定是个两端口器件,随便拿两个导体来讨论特性阻抗是没有意义的。
满足上面三个前提后,我们再看看特性阻抗的物理意义:
我们知道波的速度是有限的,最大就是真空光速,在传输线中则更慢一些,也就是说,从传输线一端加一个1V的阶跃信号(如果不懂阶跃信号,就想象传输线上本来没电,两根导体不连接但电势差为0,现在给两根导体之间加一个1V的电压),那么从信号发出,到传输线的另一端测量到这个信号会有一些延迟,延迟与传输线长度成正比,那么对于激励源来说,在信号发出后,但还未到达另一端这段时间内发生了什么呢?
传输线两根导体之间存在分布电容,由于传输线是均匀的,那么单位长度上的分布电容容值是相同的,当1V的电压上升沿沿传输线向前推进的过程中,信号前方是没有充电的分布电容,后方是充到1V的电容,既有越来越多的电容被充到1V,给这些电容充电需要激励源提供电流,由于传输线是均匀的,信号向前推进的速度也是固定的,所以单位时间内需要充电的分布电容容值也是恒定的,这意味着激励源需要提供的电流是恒定的。
已知阶跃信号的电压是1V,在阶跃信号传输过程中激励源需要提供一个恒定的电流I,这个I的大小只取决于传输线的横截面特性,那么传输线的特性阻抗R=1V/I。
工程上通常把传输线的特性阻抗设计为50欧或者75欧,就这样,传输线便有了一个与长度无关,与横截面有关的特性阻抗。
传输线末端的反射
当阶跃信号的沿到达传输线末端,如果传输线末端开路,会发生什么呢?
前面说特性阻抗的物理意义,提到了“波速有限”和“分布电容”但没有提“分布电感”,实际上正因为分布电感和分布电容同时存在,他们在单位长度上的时间常数决定了这根传输线中的波速,这才导致了“波速有限”这个结果,这几个物理量总是同时存在的,不好说哪个是因哪个是果,以我有限的知识和直觉,我只能说这可能有更深层次的物理学原理。
由于分布电感的存在,传输线上的电流不能突然变为0,这意味着末端的分布电容会被充到更高的电压,使得末端附近的分布电感两端电压反向,反向电压先减弱了正向电流,紧接着便使得电流反向,从宏观上来看,就是阶跃信号被反射回去了。
两个同频正弦信号的比是一个复数
前面说到阶跃信号在传输线末端会发生反射,实际上任何形式的信号在传输线末端都会发生反射,其中研究正弦信号的反射具有重要意义,因为根据傅里叶提出的相关理论,在数学上证明了任何能量信号均可以表示为一组正弦信号的和。
对于正弦信号的反射,显然反射信号与入射信号同频,如何比较同频正弦信号呢?
事实上在射频领域,我们经常需要比较两个同频正弦信号,除了上述反射信号,还有通过线性系统的输入和输出信号,也是同频的,此外还有电容、电感和电阻两端的电压和通过它的电流,如果电压是正弦信号,那么电流也是同频的正弦信号。
不妨设其中一个正弦信号的幅度为1,初相为0:
另一个信号可以表示为:
上面两个信号,在任何时刻(t取任意值)都有恒定的幅度之比A和恒定的相位差θ,因此两个同频正弦信之比与t无关,我们暂且将其表示为:
注意到两个信号之比的运算规则为幅度作商,相位作差,符合极坐标向量的运算规格,因此使用一个指数形式的复数来表示两个实信号之比是可能的:
上述复数也可以通过欧拉公式换算为a+bj的形式:
其中:
至此,我们明确了两个同频正弦信号之比可以用一个复数来表示,而复数有“幅度、角度”和“实部、虚部”两种表示方法,两种表示在数学上是等价的。
我们知道电容和电感是储能元件,不会耗散电功率,若以正弦信号作为激励,其物理意义就是在某半个周期储能,而在下半个周期释放能量,其电压和电流总是相差90度,因此其电压和电流之比(即阻抗),相位差总是90度(电感)或者-90度(电容),在复平面上位于虚轴上,因此电容和电感的阻抗都是纯虚数,其中电感的阻抗是正虚数,电容的阻抗是复虚数。
当正弦电压作用于电阻器时,电压和电流同相,因此电阻器的阻抗是正实数。
若存在一种元件,当正弦电压作用于其两端时,其电压与电流反相,那这种元件实际上是对外输出电功率的,因此这种元件必然含有电源,换句话说,无源网络(即阻容感的任意连接组合)的阻抗实部不小于0。
前面说到传输线末端会发生反射,若传输线末端接一个负载,反射的同时也有一部分能量被负载吸收。
反射系数Γ定义为反射信号和入射信号的比。
在如上图所示的电路中,在传输线和负载的连接点有a, b两点,以b点为0电势参考点,考虑a点,则a点上的入射电压Ui和从左向右电流Ii,也有反射电压Ur和从右向左的反射电流Ir, 根据a点左右两侧的电压和电流的连续性,有:
因为入射和反射信号都在传输线上,传输线的特性阻抗为Z0,而UL在负载两端,根据欧姆定律:
反射系数Γ定义为反射信号和入射信号的比,联立上述5个方程,不难得到:
A
工程上通常将Z0设计为一个常数,通常是50欧,在这种情况下,负载的反射系数Γ与ZL实际上是一一对应的关系,其映射关系便是:
即当Z0=50Ω时,传输线上的反射信号与入射信号之比只与负载阻抗ZL相关,与入射信号无关。
史密斯圆图
上节说到工程上将Z0设计成50欧,负载的阻抗和其反射系数是一一对应的,可以相互换算,换算关系为:
前面也提到了对于无源负载来说,ZL的实部不小于0,即ZL的取值范围是包括虚轴在内的右边半个复平面:
那么反射系数Γ的取值范围就可以计算出来:
不难证明反射系数的模小于等于1,当且仅当a=0时,|Γ|=1,当ZL=50时,Γ=0。
即无源负载的阻抗分布在包括虚轴在内的右边半个复平面,其反射系数映射到一个半径为1的圆内,并且Z平面的虚轴映射到Γ平面模为1的圆上,Z平面的50+0j映射到Γ平面的原点(圆心)。
如此,我们可以用一个动图直观地展示Z平面变换到Γ平面的过程,开始之前,我们在Z平面画出虚部(可正可负)和实部(只能为正)分别等于0、10、20、50、100、250的几条线,观察它们变换到Z平面后的状态:
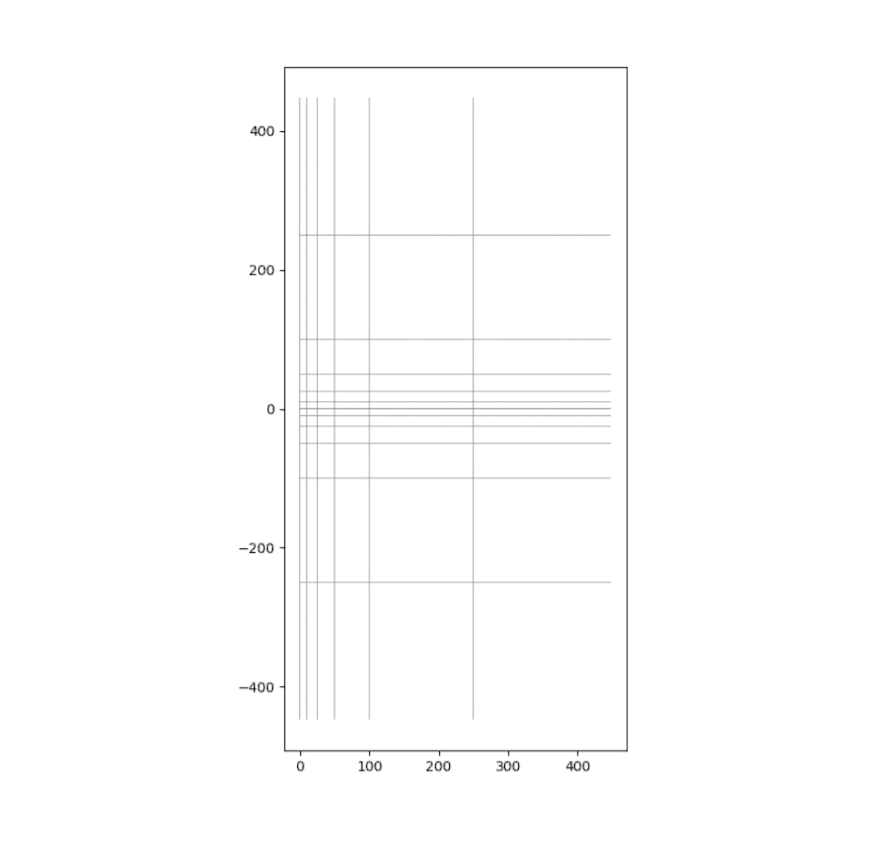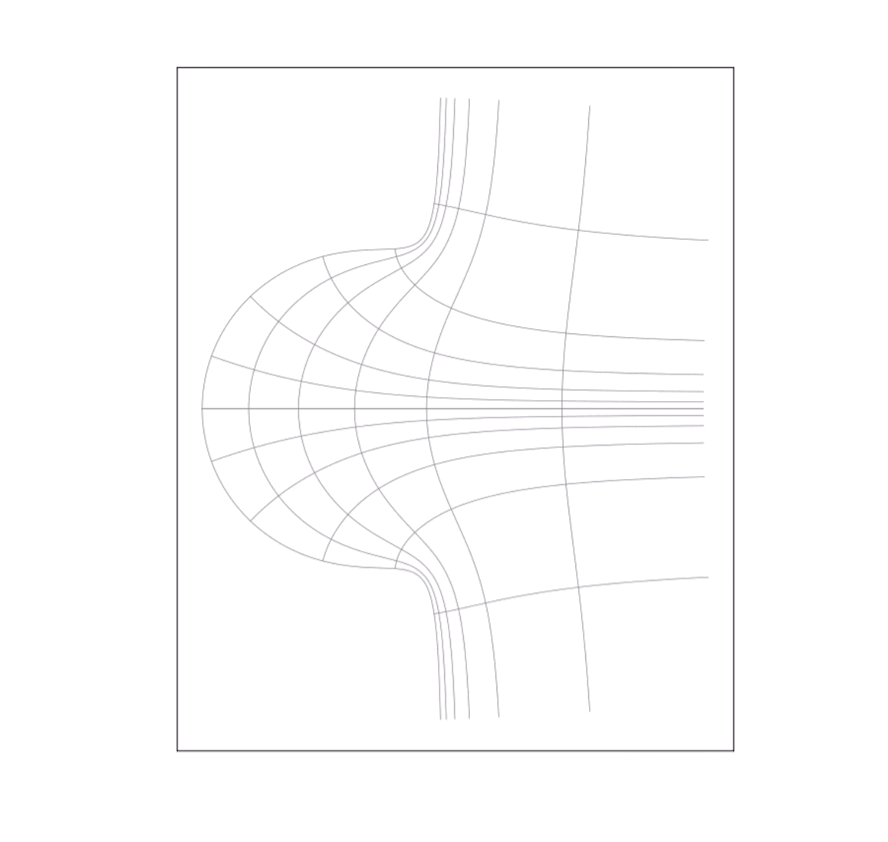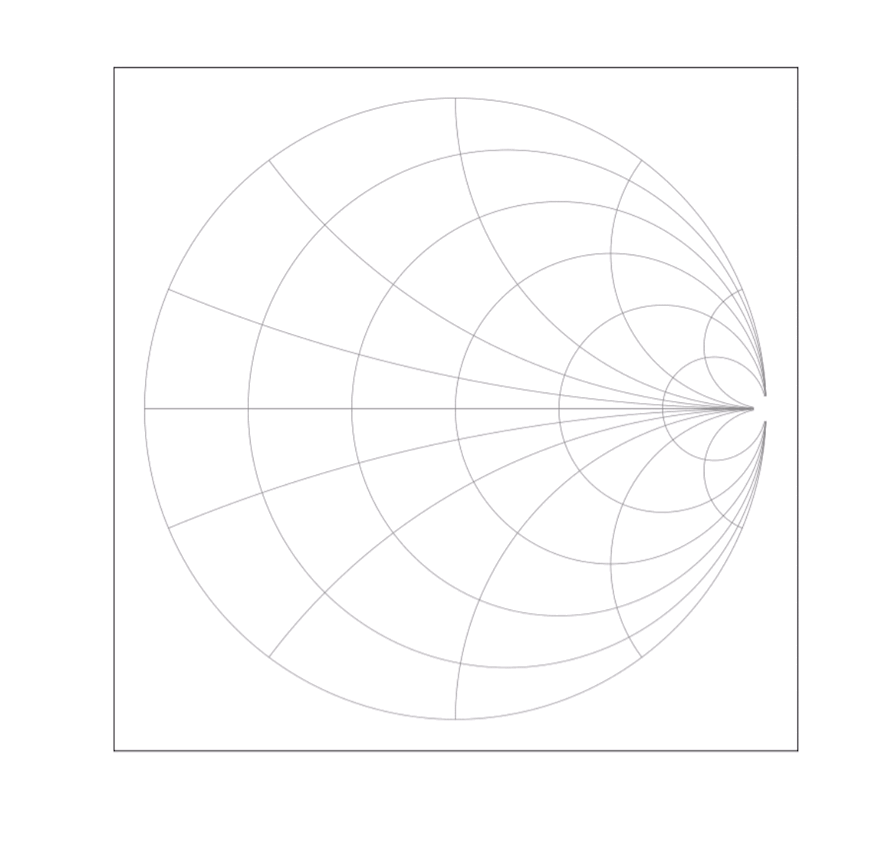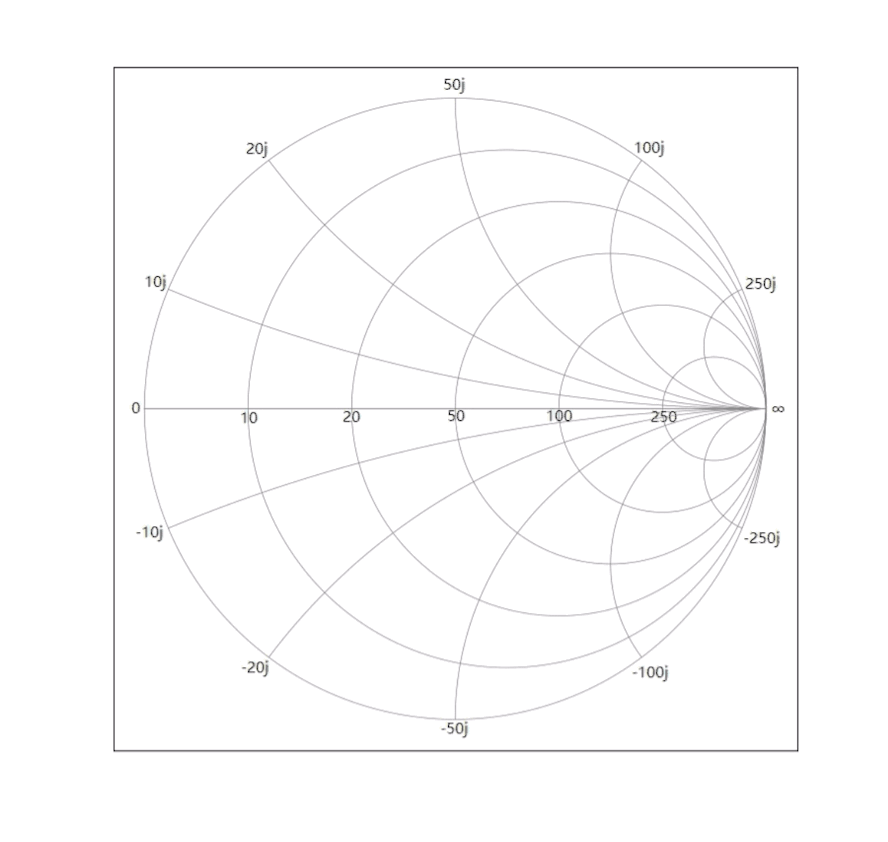
注意:该动画旨在形象地说明变换前后的映射关系,中间的过程并没有物理意义。
至此,我们便得到了史密斯圆图的阻抗形式,即史密斯阻抗圆图的物理意义就是把Z平面某些特定值的水平线和垂直线绘制在Γ平面内。其之所以表现为一个圆,是因为无源阻抗的反射系数取值范围是一个圆。
相比于无限大的Z平面,使用有限大小的史密斯圆图来绘制负载特性,不仅更加直观,也更加方便计算VSWR等其他指标,或者用于计算阻抗变换过程中所需的LRC取值。
下图便是一个无源阻抗变换的计算实例,通过电脑软件,可以轻松算出所需的匹配元件取值:
写在最后
我们在中学就学过导体是等势体,导体内部处处电势相等,工作后我们说一根线上的电压是多少V,不会特地指明这根线的什么位置是多少V,因为整根线都是一样的,但这只是静态电场下的情况,或者说是低速变化电场下的近似情况。
就好比我们说因为水是流体所以水面是平的,这似乎是个正确的理论,并且多数情况下这是没有问题的,然而它却解释不了波浪。同样的,射频领域研究的电学规律类似于波浪在水面的规律。当高频信号作用于传输线,传输线上各点的电压都不同,犹如微风在平静的水面吹起了波纹,波纹碰到岩壁发生了反射,由此产生的一系列问题等着我们去解答。
用试管研究水是看不见波浪的,只有走向汪洋大海才能体会到波澜壮阔,旅行者一号在65亿公里外,用22W的发射机和抛物面天线,艰难地向地球发出了微弱的电波,电波所到之处便是真正的星辰大海,这是射频技术的浪漫。